References

• Bobis, J., Mulligan, J., and Lowrie, T. (2008). Ch 9: Promoting Number Sense: Beyond Computation. In J. Bobis, J. Mulligan and T. Lowrie (Eds), Mathematics for children : challenging children to think mathematically (p. 215-242). Frenchs Forest, NSW: Pearson Education Australia.

• Bobis, Janette. (1996). Ch 1 : Visualisation and the Development of Number Sense with Kindergarten Children. In Mulligan, Joanne and Mitchelmore, Michael (Eds), Children's number learning (p. 17-33). Adelaide, SA: Australian Association of Mathematics Teachers. http://www.designedinstruction.com/prekorner/early-childhood-counting.html.

• Clements, D. & Sarama, J. (2000). The earliest geometry. Teaching children mathematics, 7(October), p. 82-86.
• Gelman, R. and Gallistel, C. (1992). Preverbal and verbal counting and computation.Cognition, 44(1), p. 43-74.

Subitising

'Subitising is the instant recognition of numericy in a group' (Clements, 1999). This means that children are able to recognize the numbers without counting. There are two forms of subitising:

1. Perceptual subitising.

"Recognizing a number without using other mathematical processes" (Clements 1999,p. 401).

For example if the teacher shows two oranges on the board and ask the children how many oranges are there, the children may be able to show two with their hands and say 'Two'.  The children may not have to count the number of oranges but somehow they are able to see that there are two oranges.

    2. Conceptual subitising.
"Recognizing the number pattern a s a composite of parts and as a whole, for example: an eight-dot domino" (Clements, 1999,p.401).  

Children may see the number 5 without even having to count the number  shown on the dice.

A game we all played during workshop 2.

     

Computation

Computation is the term used to describe any type of information processing (Bobis, Mulligan & Lowrie, 2008).  It involves using a mathematical operation to solve a numerical problem (Origo, 2008).  As teachers, we must put emphasis on the role of children's thinking in their mathematics learning, and build curriculum based on the development of children's concepts (Ell, 2002).  Computation can be separated into 2 categories: computation using tools, and mental computation, the ability to calculate an exact numerical answer without the use of calculating tools (Origo, 2008).

Let's take a look at computation using tools, the first phase of computation.  Teachers can use representations to assist in the development of strategies.  In mathematics, we use representations extensively, as they form a concrete image of the problem in the students mind.  In the classroom, teachers can utilise tens frames, hundreds charts or number lines to represent problems to the students.  

A strategy like this will assist early childhood students in adding and subtracting numbers using mental computation.  During these activities, the teacher could use  some of the following questions to evaluate students understanding too:

• How did you solve that? Show us/tell us
• Did anyone else solve it that way?
• How is it the same?
• Who did it differently?
• How is that different?
• What do you think about those strategies?

Counting

When an understanding of numerals has been acquired by the students, teachers will begin to teach the process of reciting numbers in a particular order, or counting.  Gelman and Gallistel (1992) state that counting involves a number of different principles.  The most common ones are one-to-one principle, stable-order principle, cardinal principle, abstraction principle and order-irrelevance principle.  Teachers may use the following learning experiences to develop the students’ ability to count. 

One-to-one principle: When counting, only one number word is assigned to each object. 

Stable-order principle: When counting, number words are always assigned in the same order. 

Cardinal principle: Having knowledge that the last number name said describes the total quantity.

Order-irrelevance principle: When counting the number of objects in a set, the order they are counted is irrelevant, as long as each object is counted.

Abstraction principle: Students realise that numbers can be used to count anything.  

Below is a link to a website that helps students to count.
http://www.abc.net.au/countusin/

Teachers can use resources like this in their classroom to ensure learners grasp their first step in Maths and able to count at early age.  

Number Types

Understanding of number is one aspect of mathematics that we expect children to develop in schools (Bobis, 1996, p.17).  Bobis (1996) states that number sense refers to “a well organised conceptual network of number information that enables a person to understand numbers and number relationships and to solve mathematical problems in ways that are not bound by traditional algorithms” (p.18). According to Berk (2009), number sense is also a skill that needs to be developed from a young age so that the children will develop their mental reasoning and cognitively flexibility earlier. In short, number sense is the ability to understand and use numbers and operations flexibly to solve mathematical problems. 

The four different types of numbers that must be recognised and developed through the early years are:

• cardinal numbers
• ordinal numbers
• whole numbers 
• integers 

Cardinal numbers are primarily used to count the number of objects in a set.  Cardinal numbers tell "how many" and are also known as "counting numbers," because they show quantity (http://www.factmonster.com/ipka/A0875618.html).  For example, 6 dogs and 5 pies.

      

Ordinal numbers are used to indicate the position of an object in a numerical sequence.  Ordinal numbers tell the order of things in a set—first, second, third, etc. Ordinal numbers do not show quantity. They only show rank or position (http://www.factmonster.com/ipka/A0875618.html). For example, first and third.

Whole numbers are zero and all counting numbers that don't include fractions or decimals.  Integers are the whole unit distance between numbers on a number line.  Teachers could demonstrate this by using whole number lines.  

Reflection for Workshop 1

Learning Mathematics was never easy for me.  I had the perception that solving Maths is just like solving a jigsaw puzzle where I need to put each and every jigsaw piece at the right place to create the beautiful picture.  I wondered how I will teach Maths to young children when I, myself, use to dislike Maths when I was young.  I was also quite surprise that there diversity in terms of how we count in our workshop and that there were only 3 other students who counts like me in the workshop. I wondered which the right way to count is or should I use the same method that I was taught to develop my future students’ number sense.

Of course, where is a better start than the beginning? The first workshop was really useful as I learnt a lot about the beginning processes.  We played with the materials that we would use to teach Maths to children.  I learnt that it is important for teachers to scaffold their learners while they are at the beginning processes by providing enough materials and verbal encouragement in order to motivate them in Maths.  The beginning is important as it determines what we will do next, therefore, it is important for children to enjoy Maths as much as they can at the beginning processes so that they can continue their journey in Maths in a more enthused manner.

I also learnt that using real life situations is important for learner to grasp Maths at young age.  As a future teacher in Malaysia, I will try to cater to the diversity of students and provide culturally suitable materials and real world situation to teach Maths.  In that way, my students will be able to learn Maths better by relating to what they learn in their classrooms to their experience of their own.

I hope to learn more in the coming weeks and hopefully more on how to teach Maths effectively to cater for diversity in the classrooms like in Malaysia.  

Beginning Processes in Mathematics

Irons (1999) suggested that the best way to introduce mathematics to young children is by establishing the mathematical concepts through “learning experiences”.  These learning experiences should encourage children to use language to describe and interpret meaning by interacting with the environment.  The learning experiences can also be described as “processes” and is the most important factor that sets the foundation for mathematics.  Teaching the beginning processes in mathematics is essential to ensure young learners have a good grasp of basics in mathematics.  Learners will be able to interpret and comprehend the integral part of mathematics through the activities that requires the use of senses. 

Identifying and describing attributes

This is a “process of highlighting and explaining attributes in relation to their similarities or differences” (Irons, 1999, p. 27). Teacher should encourage children to use wide range of language as it will help to promote reasoning at a very young age.  For example, children may be playing with two toy cars that are same is shapes and size but different in colours.  Teachers should encourage them to use their senses and identify the differences between the two trucks and use language to talk about it as they play. 

                               

Matching

Matching activities focuses on the “sameness of attributes” (Irons, 1999, p.27).  Children will have to arrange objects according to the objects’ attributes like colour, shapes, number of objects and size of the objects. During this activity, it is important for teachers to ask questions like ‘Why does this match?’ to extend children’s thinking and reasoning.  This type of questioning may help to lower the “affective filter” of the young learners and motivate them to participate actively in classroom (Krashen, 1982, p.64). 

 

Sorting

Irons (1999) defines sorting as a process involving matching, but with a greater number of objects”. The process of sorting involves grouping objects or pictures according to one or more attributes.  For this activity, teachers can plan for the children to sort things by one attribute first and later proceed to a more difficult activity, which is sorting by two or more attribute.  Teacher scaffold also plays an important role here as it helps the children to reach a stage of development that will prepare them for more complicated tasks (Vygotsky, 1964 in Berk, 2009). 

Comparing

Children will be comparing based on the amount of one attribute that is possessed by two objects (Irons, 1999).  Children are required to determine which object has more or less of the attributes and use language to compare the two objects. Their vocabulary can be highly developed during this process as their vocabulary bank can be expended when they are younger (Jenkins, 2003).  The teacher needs to address that comparison is relative and it may change or have more than one relationship so that children can understand that comparison is relative and not rigid within a context only.

Ordering

The process of ordering involves “arranging objects, pictures, groups, or events according to the relations between them based in increasing or decreasing amounts of an attribute” (Irons, 1999, p. 30).  According to Berk (2009), it is vital for teachers to use real world objects and experience during this process as learners that learners can connect with outside their classrooms.  This can be further supported by Irons (1999) who claims that young children learn best when their learning experiences involves their real life experiences because they can see a purpose of learning. Basically, children need to be able to identify, describe attributes, detect differences and make comparisons in order to do ordering. 

  

Patterning

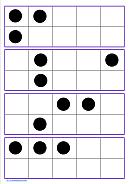
“Patterns are formed by the repetition of objects or pictures, and are recognizable and predictable” (Irons, 1999, p. 31).  In general, there are three types of patterns:

o   Repeating

o   Growing

o   relationship

Patterning forces children to draw on skills such as observing, analysing and predicting.  As stated by Irons (1999) “patterning activities help children develop confidence when they are faced with problems to solve” (p.31).

 

All these beginning processes provide a solid basis for children to “decipher” and understand the world which they live in.  Teachers should design and plan interesting activities that will expose the children to mathematics and give them the opportunity to develop their potentials to learn and enjoy mathematics. 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

References

Berk, L.E. (2009). Child Development (8th Ed). United States of America: Pearson Education.

Irons, R. R. (1999). Numeracy in early childhood educating young children. Learning and Teaching in the Early Childhood Years, 5 (3), 26-32. Retrieved from Queensland University of Technology Course Materials Database.

Jenkins, J. (2003). World Englishes. New York: Routledge Taylor & Francis Group.

Krashen, S. (1982). Second language acquisition and second language learning. New York: Pergamon Press.