Workshop 4 and 5

The assignment for workshop 4 and 5 are submitted through Assignment Minder.

Thank you.

Deeviya Nambbiar Prabhakaran

References: ALGEBRA

Economopoulos, K. (1998). What comes next?  The mathematics of pattern in kindergarden. Teaching children mathematics, 5(4), p. 230-233.

Heirdsfield, A. (2011). EAB023 Algebra [Lecture Notes]. Retrieved from http://blackboard.qut.edu.au/webapps/portal/frameset.jsp?tab_tab_group_id=_2_1&url=%2Fwebapps%2Fblackboard%2Fexecute%2Flauncher%3Ftype%3DCourse%26id%3D_75366_1%26url%3D

Queensland Studies Authority. (2008). Mathematics - Essential learnings.  Retrieved September 24, 2010, fromhttp://www.qsa.qld.edu.au/downloads/early_middle/qcar_el_maths_kau.pdf 

The Origo Handbook of Mathematics Education. (2007). QLD: Origo Education.

Willoughby, S. (1997). Functions from kindergarden through sixth grade. Teaching children mathematics, 3(6), p. 314-318.

ALL ABOUT ALGEBRA

Algebra

Algebra is the sub-strand of mathematics that uses rules to describe the relationships between quantities and events (Origo, 2008, p. 2).  Two of the most important aspects of algebra are patterns and functions.

Patterns are best described as an arrangement of shapes or numbers that repeat or change in a predictable manner (Origo, 2008, p. 75). Three types of patterns we looked at through the tutorial were: repeating patterns, growing patterns, and relationship patterns.  Economopoulos (1998, p. 230) states that from kindergarten, children should focus on regularity and repetition in motion, colour, sound, position, and quantity, and be involved in recognising, describing, extending, transferring, translating and creating patterns. The understanding of patterns should be developed at an early age, over 7 stages which assist in developing the students’ comprehension of this concept.  Stages can be broken down as:

• Look for patterns;
• Participate in building a pattern;
• Copy a pattern;
• Create a pattern;
• Extend a pattern;
• Find the missing element;
• Translate a pattern.

The Queensland Studies Authority (QSA) state that students by the end of year 3 should understand that "number patterns and sequences based on simple rules involve repetition, order and regular increases or decreases" (QSA, 2008).  Therefore, students should be exposed to and form an understanding of these stages of what patterns look like and how they work by the end of year 3.

Repeating patterns have an element which is repeated without alteration, known as the "core".  A numerical example may look as follows:

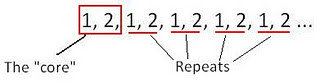
Using this example, teachers could incorporate the 7 stages into learning experieces for students to assist in developing comprehension.  When looking for patterns, students should first identify the core to understand what is being repeated. In the above example, the core is 1, 2.  When developing examples for students, teachers should ensure the core has been repeated at least 3 times and can be easily identified.  The repeats are commonly known as "terms".  By recognising the core, students will then be able to describe the pattern.  In the example below, students could describe the core asgrey circle, white square, and describe the pattern as grey circle, white square, grey circle, white square, grey circle, white square, grey circle, white square.

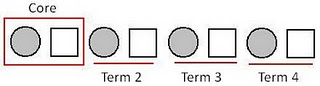
Next may involve students extending the pattern.  Now they have identified the core, and can see how the core is repeated, they could continue the rule.  Teachers should be given the opportunity to ask focus question throughout this stage.  By extending the pattern to 10 terms, and removing the 7th term, students may be asked to supply the missing parts.  Alternatively, teacher could ask what the 10th term is, 15th term, 20th term, 50th term.  Finally, students can now translate the pattern.  They can identify the rules and change the elements into other parts.  This involves "translating" which means changing the appearance of an element while maintaining the arrangement of the elements (Origo, 2008, p. 75).  An example of this would be the 2 patterns above.  Although physically they look different, the pattern repeats the same rule through both.

Growing patterns occur when elements increase or decrease. The two examples below illustrate how growing patters can be represented.

Using aspects of the 7 stages, tasks can be set for students to better understand growing patterns.  These may include:

• "What is the core in this pattern?"
• "Describe the pattern?"
• "What would the 5th term look like?  6th term?  10th term?"
• "How would you translate this pattern?"

Finally, relationship patterns occur between 2 or more sets of numbers.  The properties of 1 set affect the properties of the other set.  An example of this can be seen in the table below.  The elements in column B are 4 times the value of those in column A.

In this example, column A represents the term number, with term 1 being the core.  Column B shows what the term looks like.  If this table was to be expanded into a numeric line pattern, it would look like: 

Students can be given the opportunity explore this pattern.  Comparing the 2 columns, students should look at the following aspects of the 7 stages:

• "What is the relationship between column A and column B?"
• "Describe the pattern?"
• "What would the 6th term look like?  10th term?  20th term?
• "How would you translate this pattern?"

Functions are rules that describe the relationship between two sets of numbers (Origo, 2008, p. 43).  One set of numbers is the values of the independent variable (input), where the other set is the values of the dependent variable (output).  Functions recognise how "things" change in relation to each other.  Students will initially be introduced to functions in prep, where they use concrete representations in function activities.  Over the next years, as they move towards year 6, they gradually move from the concrete to the abstract (Willoughby, 1997, p. 314).

A great tool we used through tutorial exercises to show how functions work was the "function machine".  The function machine clearly illustrates how we start with something, and end with something different.  The example seen below represents a function machine we would use for students in a prep to year 1 level.  Concrete representations are used.  We start with a green circle.  The green circle moves through the function machine and comes out a green triangle.  We then start with a yellow circle.  The yellow circle moves through the function machine and comes out a yellow triangle.  We then have a blue circle.  If it goes through the function machine, how will it come out?  Similarly, what do we start with if it goes through the function machine and comes out a red triangle?  Students will find that the function changes circles to triangles, and keeps the colour the same.

Learning experiences such as this clearly demonstrate to students how functions work, utilising language and experiences relative to them.  As the student moves through the years, functions will begin to move from the concrete to the abstract, and finally, standard representation (Willoughby, 1997, p. 314).  The example below illustrates the function machine where standard representations are used.  We start with the number 2.  The number 2 moves through the function machine and comes out as number 5.  We then start with the number 4.  The number 4 moves through the function machine and come out the number 9.  Similarly, we start with the number 7.  The number 7 moves through the function machine and come out the number 15.  Students will find that the function doubles the number that goes into the machine (input), and adds 1, to give a number on the other end (output).  What about if the input is 9?  Using the function, how will it come out the other end?

Another aspect of functions is Equals as balance - equalities and inequalities.  Equality (shown by the symbol =) occurs when 2 or more objects or expressions are identical in a particular attribute that can be counted or measured (Origo, 2008, p. 35).  Inequality (shown by the symbol ≠) occurs when 2 or more expressions are not equal (Origo, 2008, p. 35).  Students can be introduced to "greater than" (>) and "less than" (<) while learning inequalities. Through tutorial activities, we used scales to assist in representing these functions.  These exercises can be used as appropriate learning experiences for students in early years schooling.  In the example below, we have a set of scales with 4 red balls and 5 green balls in the left basket, with 2 green balls in the right basket.  By looking at the equation below (4 + 5 = 2 + ?) we know that both sides equal each other, as the function is equality.

A question could be posed to the students, "How many red balls do I need in the right basket to balance the scales?".  By adding the contents in the left basket (4 + 5) and arriving at 9, students can see that 9 - 2 = 7, and that they will need 7 red balls to balance the scales. From here, students can gain an understanding that 4 + 5 = 2 + 7.

Alternatively, in the example below, we have been supplied with a set on unbalanced scales. These scales represent inequality as both sides are not equal.

Below the scales there are 2 set of functions.  The first (8 ≠ 3) represents the fact that both sides of the scale are not equal.

Students can use the concrete representations in the scales to recognise this.  The second demonstrates how one side of the scales is "greater than" the other.  By writing the function 8 > 3 we can see how the basket with 8 red balls outweighs the basket with 3 red balls.  Similarly, we could also write the function 3 < 8, where we use the "less than" sign to describe the basket with 3 red balls.