Workshop 4 and 5

The assignment for workshop 4 and 5 are submitted through Assignment Minder.

Thank you.

Deeviya Nambbiar Prabhakaran

References: ALGEBRA

Economopoulos, K. (1998). What comes next?  The mathematics of pattern in kindergarden. Teaching children mathematics, 5(4), p. 230-233.

Heirdsfield, A. (2011). EAB023 Algebra [Lecture Notes]. Retrieved from http://blackboard.qut.edu.au/webapps/portal/frameset.jsp?tab_tab_group_id=_2_1&url=%2Fwebapps%2Fblackboard%2Fexecute%2Flauncher%3Ftype%3DCourse%26id%3D_75366_1%26url%3D

Queensland Studies Authority. (2008). Mathematics - Essential learnings.  Retrieved September 24, 2010, fromhttp://www.qsa.qld.edu.au/downloads/early_middle/qcar_el_maths_kau.pdf 

The Origo Handbook of Mathematics Education. (2007). QLD: Origo Education.

Willoughby, S. (1997). Functions from kindergarden through sixth grade. Teaching children mathematics, 3(6), p. 314-318.

ALL ABOUT ALGEBRA

Algebra

Algebra is the sub-strand of mathematics that uses rules to describe the relationships between quantities and events (Origo, 2008, p. 2).  Two of the most important aspects of algebra are patterns and functions.

Patterns are best described as an arrangement of shapes or numbers that repeat or change in a predictable manner (Origo, 2008, p. 75). Three types of patterns we looked at through the tutorial were: repeating patterns, growing patterns, and relationship patterns.  Economopoulos (1998, p. 230) states that from kindergarten, children should focus on regularity and repetition in motion, colour, sound, position, and quantity, and be involved in recognising, describing, extending, transferring, translating and creating patterns. The understanding of patterns should be developed at an early age, over 7 stages which assist in developing the students’ comprehension of this concept.  Stages can be broken down as:

• Look for patterns;
• Participate in building a pattern;
• Copy a pattern;
• Create a pattern;
• Extend a pattern;
• Find the missing element;
• Translate a pattern.

The Queensland Studies Authority (QSA) state that students by the end of year 3 should understand that "number patterns and sequences based on simple rules involve repetition, order and regular increases or decreases" (QSA, 2008).  Therefore, students should be exposed to and form an understanding of these stages of what patterns look like and how they work by the end of year 3.

Repeating patterns have an element which is repeated without alteration, known as the "core".  A numerical example may look as follows:

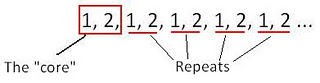
Using this example, teachers could incorporate the 7 stages into learning experieces for students to assist in developing comprehension.  When looking for patterns, students should first identify the core to understand what is being repeated. In the above example, the core is 1, 2.  When developing examples for students, teachers should ensure the core has been repeated at least 3 times and can be easily identified.  The repeats are commonly known as "terms".  By recognising the core, students will then be able to describe the pattern.  In the example below, students could describe the core asgrey circle, white square, and describe the pattern as grey circle, white square, grey circle, white square, grey circle, white square, grey circle, white square.

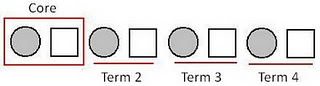
Next may involve students extending the pattern.  Now they have identified the core, and can see how the core is repeated, they could continue the rule.  Teachers should be given the opportunity to ask focus question throughout this stage.  By extending the pattern to 10 terms, and removing the 7th term, students may be asked to supply the missing parts.  Alternatively, teacher could ask what the 10th term is, 15th term, 20th term, 50th term.  Finally, students can now translate the pattern.  They can identify the rules and change the elements into other parts.  This involves "translating" which means changing the appearance of an element while maintaining the arrangement of the elements (Origo, 2008, p. 75).  An example of this would be the 2 patterns above.  Although physically they look different, the pattern repeats the same rule through both.

Growing patterns occur when elements increase or decrease. The two examples below illustrate how growing patters can be represented.

Using aspects of the 7 stages, tasks can be set for students to better understand growing patterns.  These may include:

• "What is the core in this pattern?"
• "Describe the pattern?"
• "What would the 5th term look like?  6th term?  10th term?"
• "How would you translate this pattern?"

Finally, relationship patterns occur between 2 or more sets of numbers.  The properties of 1 set affect the properties of the other set.  An example of this can be seen in the table below.  The elements in column B are 4 times the value of those in column A.

In this example, column A represents the term number, with term 1 being the core.  Column B shows what the term looks like.  If this table was to be expanded into a numeric line pattern, it would look like: 

Students can be given the opportunity explore this pattern.  Comparing the 2 columns, students should look at the following aspects of the 7 stages:

• "What is the relationship between column A and column B?"
• "Describe the pattern?"
• "What would the 6th term look like?  10th term?  20th term?
• "How would you translate this pattern?"

Functions are rules that describe the relationship between two sets of numbers (Origo, 2008, p. 43).  One set of numbers is the values of the independent variable (input), where the other set is the values of the dependent variable (output).  Functions recognise how "things" change in relation to each other.  Students will initially be introduced to functions in prep, where they use concrete representations in function activities.  Over the next years, as they move towards year 6, they gradually move from the concrete to the abstract (Willoughby, 1997, p. 314).

A great tool we used through tutorial exercises to show how functions work was the "function machine".  The function machine clearly illustrates how we start with something, and end with something different.  The example seen below represents a function machine we would use for students in a prep to year 1 level.  Concrete representations are used.  We start with a green circle.  The green circle moves through the function machine and comes out a green triangle.  We then start with a yellow circle.  The yellow circle moves through the function machine and comes out a yellow triangle.  We then have a blue circle.  If it goes through the function machine, how will it come out?  Similarly, what do we start with if it goes through the function machine and comes out a red triangle?  Students will find that the function changes circles to triangles, and keeps the colour the same.

Learning experiences such as this clearly demonstrate to students how functions work, utilising language and experiences relative to them.  As the student moves through the years, functions will begin to move from the concrete to the abstract, and finally, standard representation (Willoughby, 1997, p. 314).  The example below illustrates the function machine where standard representations are used.  We start with the number 2.  The number 2 moves through the function machine and comes out as number 5.  We then start with the number 4.  The number 4 moves through the function machine and come out the number 9.  Similarly, we start with the number 7.  The number 7 moves through the function machine and come out the number 15.  Students will find that the function doubles the number that goes into the machine (input), and adds 1, to give a number on the other end (output).  What about if the input is 9?  Using the function, how will it come out the other end?

Another aspect of functions is Equals as balance - equalities and inequalities.  Equality (shown by the symbol =) occurs when 2 or more objects or expressions are identical in a particular attribute that can be counted or measured (Origo, 2008, p. 35).  Inequality (shown by the symbol ≠) occurs when 2 or more expressions are not equal (Origo, 2008, p. 35).  Students can be introduced to "greater than" (>) and "less than" (<) while learning inequalities. Through tutorial activities, we used scales to assist in representing these functions.  These exercises can be used as appropriate learning experiences for students in early years schooling.  In the example below, we have a set of scales with 4 red balls and 5 green balls in the left basket, with 2 green balls in the right basket.  By looking at the equation below (4 + 5 = 2 + ?) we know that both sides equal each other, as the function is equality.

A question could be posed to the students, "How many red balls do I need in the right basket to balance the scales?".  By adding the contents in the left basket (4 + 5) and arriving at 9, students can see that 9 - 2 = 7, and that they will need 7 red balls to balance the scales. From here, students can gain an understanding that 4 + 5 = 2 + 7.

Alternatively, in the example below, we have been supplied with a set on unbalanced scales. These scales represent inequality as both sides are not equal.

Below the scales there are 2 set of functions.  The first (8 ≠ 3) represents the fact that both sides of the scale are not equal.

Students can use the concrete representations in the scales to recognise this.  The second demonstrates how one side of the scales is "greater than" the other.  By writing the function 8 > 3 we can see how the basket with 8 red balls outweighs the basket with 3 red balls.  Similarly, we could also write the function 3 < 8, where we use the "less than" sign to describe the basket with 3 red balls. 

References

• Bobis, J., Mulligan, J., and Lowrie, T. (2008). Ch 9: Promoting Number Sense: Beyond Computation. In J. Bobis, J. Mulligan and T. Lowrie (Eds), Mathematics for children : challenging children to think mathematically (p. 215-242). Frenchs Forest, NSW: Pearson Education Australia.

• Bobis, Janette. (1996). Ch 1 : Visualisation and the Development of Number Sense with Kindergarten Children. In Mulligan, Joanne and Mitchelmore, Michael (Eds), Children's number learning (p. 17-33). Adelaide, SA: Australian Association of Mathematics Teachers. http://www.designedinstruction.com/prekorner/early-childhood-counting.html.

• Clements, D. & Sarama, J. (2000). The earliest geometry. Teaching children mathematics, 7(October), p. 82-86.
• Gelman, R. and Gallistel, C. (1992). Preverbal and verbal counting and computation.Cognition, 44(1), p. 43-74.

Subitising

'Subitising is the instant recognition of numericy in a group' (Clements, 1999). This means that children are able to recognize the numbers without counting. There are two forms of subitising:

1. Perceptual subitising.

"Recognizing a number without using other mathematical processes" (Clements 1999,p. 401).

For example if the teacher shows two oranges on the board and ask the children how many oranges are there, the children may be able to show two with their hands and say 'Two'.  The children may not have to count the number of oranges but somehow they are able to see that there are two oranges.

    2. Conceptual subitising.
"Recognizing the number pattern a s a composite of parts and as a whole, for example: an eight-dot domino" (Clements, 1999,p.401).  

Children may see the number 5 without even having to count the number  shown on the dice.

A game we all played during workshop 2.

     

Computation

Computation is the term used to describe any type of information processing (Bobis, Mulligan & Lowrie, 2008).  It involves using a mathematical operation to solve a numerical problem (Origo, 2008).  As teachers, we must put emphasis on the role of children's thinking in their mathematics learning, and build curriculum based on the development of children's concepts (Ell, 2002).  Computation can be separated into 2 categories: computation using tools, and mental computation, the ability to calculate an exact numerical answer without the use of calculating tools (Origo, 2008).

Let's take a look at computation using tools, the first phase of computation.  Teachers can use representations to assist in the development of strategies.  In mathematics, we use representations extensively, as they form a concrete image of the problem in the students mind.  In the classroom, teachers can utilise tens frames, hundreds charts or number lines to represent problems to the students.  

A strategy like this will assist early childhood students in adding and subtracting numbers using mental computation.  During these activities, the teacher could use  some of the following questions to evaluate students understanding too:

• How did you solve that? Show us/tell us
• Did anyone else solve it that way?
• How is it the same?
• Who did it differently?
• How is that different?
• What do you think about those strategies?

Counting

When an understanding of numerals has been acquired by the students, teachers will begin to teach the process of reciting numbers in a particular order, or counting.  Gelman and Gallistel (1992) state that counting involves a number of different principles.  The most common ones are one-to-one principle, stable-order principle, cardinal principle, abstraction principle and order-irrelevance principle.  Teachers may use the following learning experiences to develop the students’ ability to count. 

One-to-one principle: When counting, only one number word is assigned to each object. 

Stable-order principle: When counting, number words are always assigned in the same order. 

Cardinal principle: Having knowledge that the last number name said describes the total quantity.

Order-irrelevance principle: When counting the number of objects in a set, the order they are counted is irrelevant, as long as each object is counted.

Abstraction principle: Students realise that numbers can be used to count anything.  

Below is a link to a website that helps students to count.
http://www.abc.net.au/countusin/

Teachers can use resources like this in their classroom to ensure learners grasp their first step in Maths and able to count at early age.  

Number Types

Understanding of number is one aspect of mathematics that we expect children to develop in schools (Bobis, 1996, p.17).  Bobis (1996) states that number sense refers to “a well organised conceptual network of number information that enables a person to understand numbers and number relationships and to solve mathematical problems in ways that are not bound by traditional algorithms” (p.18). According to Berk (2009), number sense is also a skill that needs to be developed from a young age so that the children will develop their mental reasoning and cognitively flexibility earlier. In short, number sense is the ability to understand and use numbers and operations flexibly to solve mathematical problems. 

The four different types of numbers that must be recognised and developed through the early years are:

• cardinal numbers
• ordinal numbers
• whole numbers 
• integers 

Cardinal numbers are primarily used to count the number of objects in a set.  Cardinal numbers tell "how many" and are also known as "counting numbers," because they show quantity (http://www.factmonster.com/ipka/A0875618.html).  For example, 6 dogs and 5 pies.

      

Ordinal numbers are used to indicate the position of an object in a numerical sequence.  Ordinal numbers tell the order of things in a set—first, second, third, etc. Ordinal numbers do not show quantity. They only show rank or position (http://www.factmonster.com/ipka/A0875618.html). For example, first and third.

Whole numbers are zero and all counting numbers that don't include fractions or decimals.  Integers are the whole unit distance between numbers on a number line.  Teachers could demonstrate this by using whole number lines.  

Reflection for Workshop 1

Learning Mathematics was never easy for me.  I had the perception that solving Maths is just like solving a jigsaw puzzle where I need to put each and every jigsaw piece at the right place to create the beautiful picture.  I wondered how I will teach Maths to young children when I, myself, use to dislike Maths when I was young.  I was also quite surprise that there diversity in terms of how we count in our workshop and that there were only 3 other students who counts like me in the workshop. I wondered which the right way to count is or should I use the same method that I was taught to develop my future students’ number sense.

Of course, where is a better start than the beginning? The first workshop was really useful as I learnt a lot about the beginning processes.  We played with the materials that we would use to teach Maths to children.  I learnt that it is important for teachers to scaffold their learners while they are at the beginning processes by providing enough materials and verbal encouragement in order to motivate them in Maths.  The beginning is important as it determines what we will do next, therefore, it is important for children to enjoy Maths as much as they can at the beginning processes so that they can continue their journey in Maths in a more enthused manner.

I also learnt that using real life situations is important for learner to grasp Maths at young age.  As a future teacher in Malaysia, I will try to cater to the diversity of students and provide culturally suitable materials and real world situation to teach Maths.  In that way, my students will be able to learn Maths better by relating to what they learn in their classrooms to their experience of their own.

I hope to learn more in the coming weeks and hopefully more on how to teach Maths effectively to cater for diversity in the classrooms like in Malaysia.  

Beginning Processes in Mathematics

Irons (1999) suggested that the best way to introduce mathematics to young children is by establishing the mathematical concepts through “learning experiences”.  These learning experiences should encourage children to use language to describe and interpret meaning by interacting with the environment.  The learning experiences can also be described as “processes” and is the most important factor that sets the foundation for mathematics.  Teaching the beginning processes in mathematics is essential to ensure young learners have a good grasp of basics in mathematics.  Learners will be able to interpret and comprehend the integral part of mathematics through the activities that requires the use of senses. 

Identifying and describing attributes

This is a “process of highlighting and explaining attributes in relation to their similarities or differences” (Irons, 1999, p. 27). Teacher should encourage children to use wide range of language as it will help to promote reasoning at a very young age.  For example, children may be playing with two toy cars that are same is shapes and size but different in colours.  Teachers should encourage them to use their senses and identify the differences between the two trucks and use language to talk about it as they play. 

                               

Matching

Matching activities focuses on the “sameness of attributes” (Irons, 1999, p.27).  Children will have to arrange objects according to the objects’ attributes like colour, shapes, number of objects and size of the objects. During this activity, it is important for teachers to ask questions like ‘Why does this match?’ to extend children’s thinking and reasoning.  This type of questioning may help to lower the “affective filter” of the young learners and motivate them to participate actively in classroom (Krashen, 1982, p.64). 

 

Sorting

Irons (1999) defines sorting as a process involving matching, but with a greater number of objects”. The process of sorting involves grouping objects or pictures according to one or more attributes.  For this activity, teachers can plan for the children to sort things by one attribute first and later proceed to a more difficult activity, which is sorting by two or more attribute.  Teacher scaffold also plays an important role here as it helps the children to reach a stage of development that will prepare them for more complicated tasks (Vygotsky, 1964 in Berk, 2009). 

Comparing

Children will be comparing based on the amount of one attribute that is possessed by two objects (Irons, 1999).  Children are required to determine which object has more or less of the attributes and use language to compare the two objects. Their vocabulary can be highly developed during this process as their vocabulary bank can be expended when they are younger (Jenkins, 2003).  The teacher needs to address that comparison is relative and it may change or have more than one relationship so that children can understand that comparison is relative and not rigid within a context only.

Ordering

The process of ordering involves “arranging objects, pictures, groups, or events according to the relations between them based in increasing or decreasing amounts of an attribute” (Irons, 1999, p. 30).  According to Berk (2009), it is vital for teachers to use real world objects and experience during this process as learners that learners can connect with outside their classrooms.  This can be further supported by Irons (1999) who claims that young children learn best when their learning experiences involves their real life experiences because they can see a purpose of learning. Basically, children need to be able to identify, describe attributes, detect differences and make comparisons in order to do ordering. 

  

Patterning

“Patterns are formed by the repetition of objects or pictures, and are recognizable and predictable” (Irons, 1999, p. 31).  In general, there are three types of patterns:

o   Repeating

o   Growing

o   relationship

Patterning forces children to draw on skills such as observing, analysing and predicting.  As stated by Irons (1999) “patterning activities help children develop confidence when they are faced with problems to solve” (p.31).

 

All these beginning processes provide a solid basis for children to “decipher” and understand the world which they live in.  Teachers should design and plan interesting activities that will expose the children to mathematics and give them the opportunity to develop their potentials to learn and enjoy mathematics. 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

References

Berk, L.E. (2009). Child Development (8th Ed). United States of America: Pearson Education.

Irons, R. R. (1999). Numeracy in early childhood educating young children. Learning and Teaching in the Early Childhood Years, 5 (3), 26-32. Retrieved from Queensland University of Technology Course Materials Database.

Jenkins, J. (2003). World Englishes. New York: Routledge Taylor & Francis Group.

Krashen, S. (1982). Second language acquisition and second language learning. New York: Pergamon Press.